2021학년도 수능 가형 20번 어려운 이유 & 해설
2021학년도 수능 가형 20번 (by.csm).pdf
안녕하세요 CSM입니다.
20번 해설을 들고왔습니다.
현재 21번보다
체감 난이도가 높다고 여겨지는 20번입니다.
21번
체감난이도가 높은 이유는
1) 함수 g(x)의 치역설정
2) 정적분의 "결과값"을 통해 함수 개형추론
에 있어서 기존 기출에서
단단하게 연습하기 어려운 형태여서
학생들이 조금 풀기 어려워한 듯 보입니다.
먼저 교양적으로 알아야 할 사실은
아래 그림과 같이 삼각함수 반주기의
넓이(정적분값)를 빠르게 파악해야 합니다.
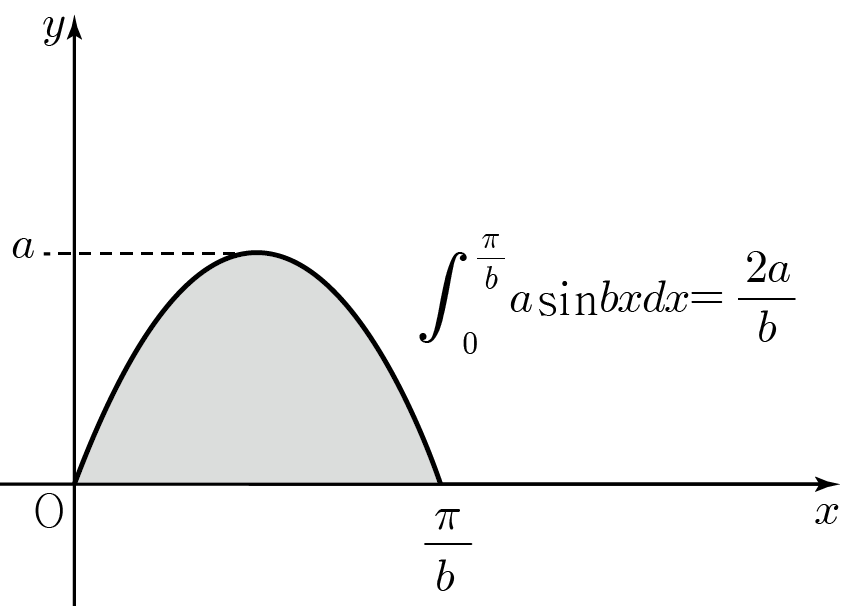
이를 토대로 해설은 다음과 같습니다. (아래 이미지 PDF도 첨부)
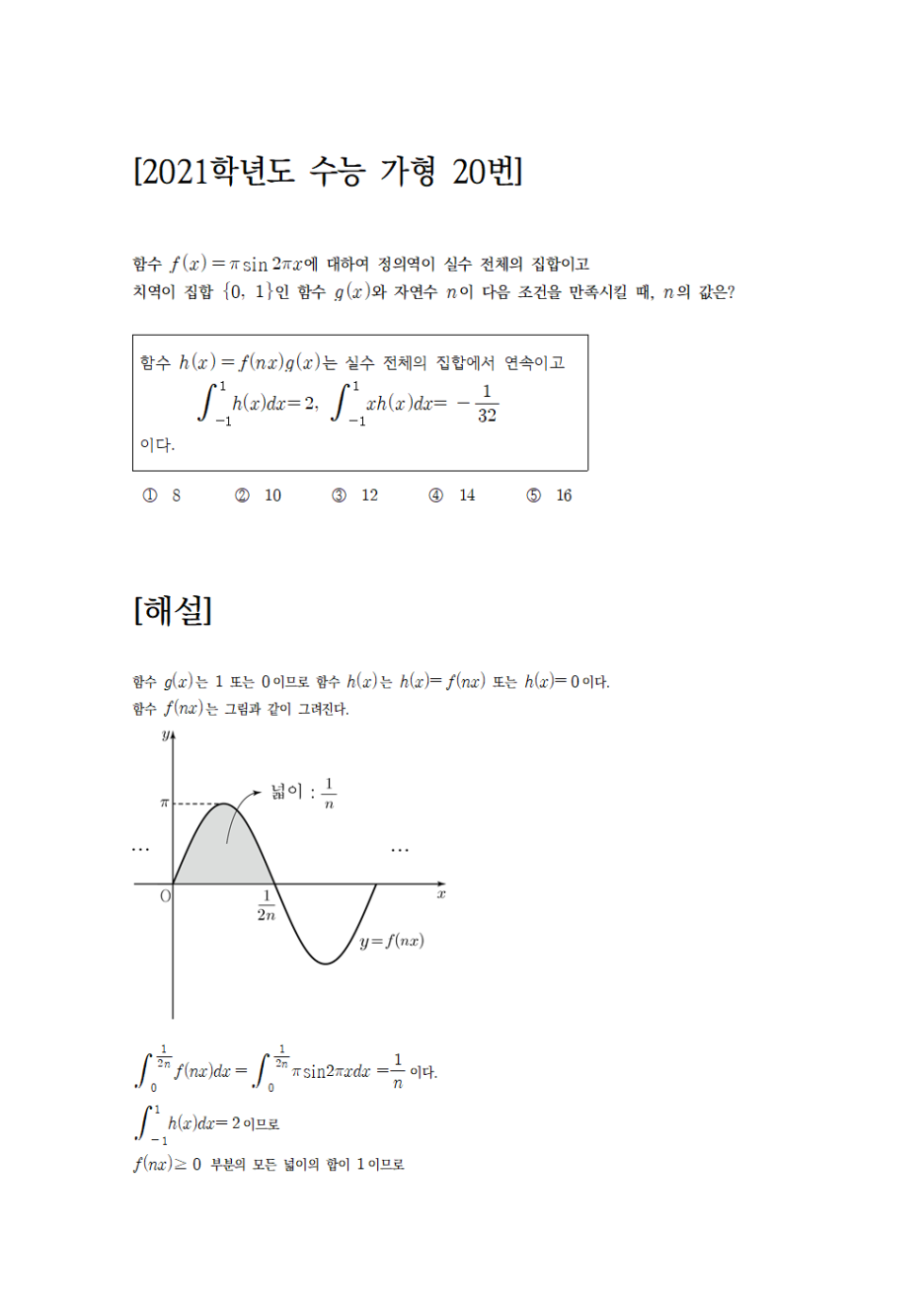
사진 설명을 입력하세요.
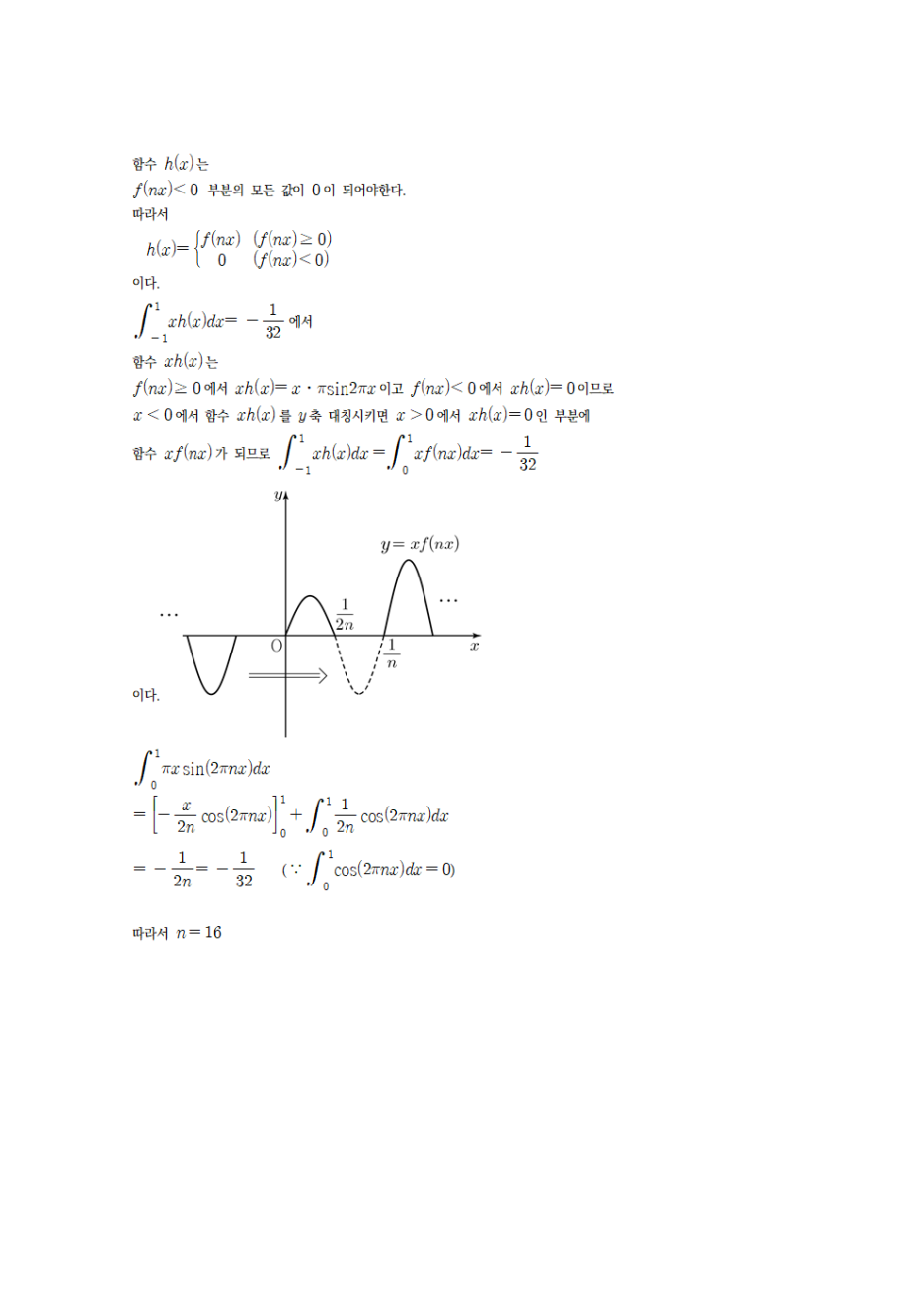
사진 설명을 입력하세요.
두가지 적분의 해석을 넓이관점과 식의 관점으로 보는 방향에 따라
풀이속도가 달라질 수 있는 문제이고 이런 경우에는
학생들에게 체감난이도 격차를 줄 수 있었던 문제라고 생각합니다.
도움이 되셨기를 바랍니다.
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
진짜 진지하게 고능아들 많이 유입될거같은데 이거 맞으려나? 6모 표본 상태 보고 함...
-
수시로 대학 갈 줄 알았으면 연논도 넣어보는 건데 ㄹㅇ 1
연논이 수능 끝나고 3주 뒤에도 있을 줄은 몰랐지
-
센츄리온이당 4
우왕
-
작년 시립대 까보니까 앞에 10명 더 들어왔었는데 연고도 비슷할까용
-
장래희망 변화 16
경비원->역사학자->피아니스트->과학자->기자->약학연구원->의사->이세카이천재미소녀
-
인하 전자전기 2
올해 신설이라는데 폭발조짐보이네… 컷이 계속오르노
-
흙수저 전형은 없음뇨?
-
중대 건설환경플랜트 공학 vs 건대 기계로봇자동차 공학 0
어디 갈까요
-
한 3,4년만에 수능을 봐야겠다고 생각하고 8월 중순부터 시작해서 이번 수능...
-
사1과1 1
사1과1로 못가는 대학이 있나요 ??
-
지구로 문자왔는데 서바는 30점대 엄청 많이받아서 왜 저한테 온건진 모르겠는데...
-
아는 문제는 어차피 풀릴거고, 열심히 공부해봤자 시험장에서 처음보는 문제 보면 시간...
-
피램같은 독학서로 다시 기출 보고 ebs랑 실모하려고 하는데 괜찮은가요? 현역때는...
-
대치동 겨울 특 4
초딩들 전부 몽클레어 패딩 입음
-
님들아 한양인터칼리지 컷 몇점 쯤으로 예상함뇨? 여기쓸지 성글경쓸지 고민하고있는데
-
충청 지역인재 가능합니다
-
슬슬 경제/과탐 특징 나타나는거같음 원랜 낚시로 수능날 나락보내는게 특성이라 조금...
-
2차추합 발표까지 D-2h38m 제발제발제발제발제발제발제발제발제발제발제발제발제발제발제발제발제발제발
-
연고대 문과 희망하고 공부 빡세게 한다는 전제하에 어떤 과목 선택이 유리할까여 화작...
-
프로 만나서 개같이 패배 진심 공부나 할까
-
ㅇㅁㅇ
-
뭐 오르비 들어오면 의대합격률이 막 올라감?
-
왜 변표 발표 안함? 돌아버리겠네
-
이번 수능 봐서 국어는 3 수학은 2인데 탐구는 아예 노베라... ㅠㅠ 제가 연세대...
-
6모 9모 수능 미적분 원점수 96 92 96 입니다 사실 재수하게 되면 수학 말고...
-
생각해보니까 시간낭비야
-
딴데보다 추합도 늦게 발표하고 2차부터 바로 전화돌리고… 진짜 너무 피말림 ㅠㅠ
-
현실에선 살면서 웃을 일이 더 많고 화낼 일이 별로 없는데 커뮤만 오면 화가 불쑥불쑥 튀어나오네
-
줘도 안 갈 곳이거나 못붙을 곳밖에 없는데 안쓰게되면 걍 원서 두장인거잖아...
-
그 순간 도파민이 어느 정도로 뿜어져 나오던가요
-
자유전공 예비 0
지금 대학들에서 자유전공을 엄청 뽑는데 그럼 예비가 많이 돌수가 있나요? 감이 안잡히네요
-
발표할거같은데 아직도 논의중이라 하는거 보면
-
오 나 뱃지달렸다 10
이야
-
돈 많은 사람이 더 좋은 제품 쓰고 사치부리겠다는데 거기에 대고 왜 ‘양극화’ 같은...
-
어떻게 아냐고? 나도 알고싶지 않았음 ….. ㅠㅠ
-
도망친 곳에 낙원은 없다
-
다시 미달 200명시절 나오나
-
종강 기념 무물 5
경한 관련 질문 받습니다! 아는 한에서 최대한 답변해드릴게유
-
수능 성적통지표로도 되나요?? 아님 증명서여야 하나요 지금 통지표밖에 없어서 귀찮은데...
-
어디든 가능? 인문 한양대 성대 성균관대 냥대식 정시 냥대 재수 삼수 현역
-
성대 변표 3
전화해본 결과 빠르면 오늘 오후 늦으면 다음주초인데 지금 변표 논의중이라고 합니다
-
수능 끝나고 음악에만 80넘게 쓴듯 가진 모든 돈을 음악에 꼴박았음 재수할 돈도 없는놈이..
-
446 4
이건 좀 오바일까요 여러분
-
넹…
-
한양대 최종컷 1
한양대 낙지 최종컷도 많이 변하나요? 평소처럼 찔끔 오르는게 아니라
-
그래 이런식으로 계속 베댓을 달면 덕코를 모을 수 있다는 거지?
-
어문만 되나?


















































개인적으로 매우 친숙한 유형은 아니라고 생각합니다. 현장기준 어려웠을 것 같아요
asinbx 한칸넓이 a/b라서 n이 2의거듭제곱만 될거같아서 1.5중에 고민하고 5번 왼쪽정적분으로 계산해보니 사인 양수는 0곱해서 없어질것같고 음수는 -1곱해져서 양수가 될것같은 느낌으로 킹리적갓심씀
ㄹㅇ 걍 찍맞이네
아니에요 킹리적갓심은 절대 그냥 나오지 않습니다. 잘하셨습니다 ^__^
해설 잘 봤어요. 마지막에 정적분 int_{-1}^{1} xh(x)dx=int_{0}^{1} xf(nx)로 넘어가는 부분이 잘 이해가 안되는데 혹시 여유있으시다면 설명해주실 수 있을까요? 저는 사진처럼 풀었는데, 계산이 무척 더럽고 현장에서 저렇게 풀면 계산실수가 반드시 있을 것 같아서 부탁드립니다....(첫 줄의 오류는 건너뛰어주세요 고치기 귀찮아서...ㅎㅎ)
in_{-1}^{0}xh(x)dx 부분만 관찰해주시면 될 것 같습니다. 함숫값이 음수인 부분은 제거 되었을것이고 양수인부분만 남은 h(x)에 대하여 x를 곱하는데 x<0이므로 xh(x)<0가 됩니다.
따라서 xh(x)를 (-1,1)에서 그린 후 각각 적분을 하여도 괜찮습니다만,
(-1,0)인 부분을 그대로 y축 대칭시켜보면 결국 xf(nx)가 완성된다는 것을 알 수 있습니다.
이는 f(nx)가 처음부터 대칭함수이고 x를 곱하여서 '대칭성질'이 남아있다고 생각하여 판단할 수 있으며 이를 (-1, 0) => (0, 1)로 이동하는 치환적분하여 식적으로도 설명가능하나 이를 계산으로 의도하기보다는 최근 "영역관찰"을 포인트 잡아왔기에 그림도 적절히 섞어서 확인해주시면 될 것 같습니다.^^
아아아아 다 그대로 대칭되니까 그렇겠네요 감사합니다.
찍는게 더 빠를 듯. 2랑 1/32 나오고 f(nx) 주기가 1/n 이니까 8, 16 처럼 2의 거듭제곱꼴로 나오는 수가 답일 것 같고 8은 너무 작아서 16했는데 아.. 계산이 엄청 빡센거였네요
진짜 시험장에서 제일 어려웠어요... 30 20 이 최고봉.
이제 21 29 은 킬러 아닌듯해여ㅜ
와.. 그냥 1/2n~1/n, 1/n~3/2n 계속 적분해가면서 귀납적으로 적분값을 찾아냈는데 y축대칭하면 한번의 적분으로 풀리네요 진짜 충격이네