★문제풀이★수학의 바이블 공통수학(상)425page 02-3예제★
02-3 다음 물음에 답하여라
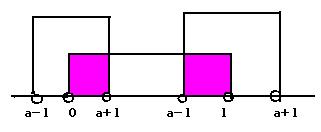애써서 그렸습니다.
(1) 0<x<1 인 모든 실수 x에 대하여 |x-a|<1 이 성립하도록 하는 실수 a의 값의 범위를 구하여라.
(2) 0<x<1 인 어떤 x에 대하여 |x-a|<1 이 성립하도록 하는 실수 a의 값의 범위를 구하여라.
------------------------------------------------------------------------------------
까지가 문제입니다.
두 문제를 풀어봤는데 답이 상이해서 다시보니 문제가 토시하나 빼고 다 똑같은데
'모든 실수x'와 '어떤 x'이 차이때문에 답이 달라집니다.
*****************************************************************************
개인적으로 처음문제(1)는 이렇게 해결했습니다.
x-1 < a, ---- ①
a < x + 1 ---- ②
에서 0 < x < 1 이므로
-1 < x -1 < 0.....①에 적용하면 -1 < x-1 < a 에서 =이 없는 <등호이므로 =사용가능
그러므로
∴0≤a 획득 --- ⓐ
1 < x + 1 < 2 ....②에 적용하면 a < x +1 < 2 에서 =없는<이므로 등호(=)사용가능
그러므로
∴a≤1 획득 --- ⓑ
.
그러므로 ⓐ, ⓑ에 의하여
∴ 0≤a≤1
라는 결론을 도출해냅니다.
이정도는 혼자서 충분히 도출해 낼 수 있는 수준이고 쉽다고 생각을 합니다.
하지만 어떤x에 대하여
라는 말한마디가 저를 미치게하는군요
개인적으로 40분가까이 한문제만 바라보게 했네요. 제가 많이 부족하다는걸 느끼게했습니다.
.
어떤소린지 이해가 가지 않았기에...
////////////////////////////////////////////
(1)은 상식의 선에서 '모든실수x'에 대해서 성립하도록 보여라
라는게 제가 여지껏 알고있는 선이었지만
(2)는 어떤실수 x라고하니 답이 완전히 달라지는데
이게 해답지를 보니 명제관련한 내용인것같지만 이해가 가지 않더군요.
해답지 관련내용은 다음과 같습니다.
|x-a|<1 에서 -1 < x-a < 1 이므로
a-1 < x < a+1
x를 중심에 둔건 저와 조금 방식이 다르지만, 여기까진 이해에 문제가 없습니다.
하지만 이후 해설★
A = { x | 0 < x < 1 }, B = { x | a-1 < x < a+1 } 이라고 한다면
(1)A⊂B 이어야 하므로
a-1≤0 이고 1 ≤ a+1
∴ 0 ≤ a ≤ 1
이부분을 명제단원을 기억해서 이해하자면
A는 B이다 라고한다면 A⊂B 이어야 하므로
(x범우) 인 모든 실수 x에 대하여 (x관련식)이 성립하도록 ▶ A이면 B이다 라고 이해가 가능합니다.
하지만
(2)A ∩ B ≠ φ (φ는 공집합) 이어야 하므로
a - 1 ≤ 0 ≤ a + 1 또는
a - 1 ≤ 1 ≤ a + 1
∴ -1 < a < 2
애써서 그렸습니다.-------------------
위와 같이 (1)과 (2)에 대해서 나외있는데
(1)에서 A⊂B 임은 이해가 가지만
(2)에서 WHY 도대체 왜 <<A ∩ B ≠ φ (φ는 공집합) 이어야 하므로 >>인지 이해가 가질 않습니다.
명제로 따지면 역인가요?
<<모든실수 x>>의 반대가 << 어떤실수 x>>인가요?
이렇게 배웠던거같은데 확인차 궁금합니다.
만약 그러했다고 하더라도
(2)의 해설에서
A ∩ B ≠ φ
이라고 해놨다면
a + 1 ≤ 0 혹은 1 ≤ a - 1
이렇게 식이 세워져야하는것 아닌가요??
도대체 왜
A ∩ B ≠ φ
라고 스스로 해놓고서
위의 그림과같이 공통부분이 있도록 만들어놨는지 이해가 가질않습니다.
통쾌한 해답 부탁드립니다.
내공 100걸게요.
http://kin.naver.com/qna/detail.nhn?d1id=11&dirId=110403&docId=163328177
에 와서 통쾌하게 이해할 수 있도록 답해주시면
네이버 내공 100 드릴게요 부탁드립니다.
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
첫번째 댓글의 주인공이 되어보세요.