4탄 추측과 정당화, 수능 12번 (부모의 마음을 가진 평가원)
[추측과 정당화 (feat. Route Finding)]

2024학년도 수능 12번
1) 문제에서 묻는 것은 "g(x)와 x축으로 둘러싸인 영역의 넓이"의 최댓값이다.
2) 그렇다면 g(x)는 무엇인가? 주어진 정보를 보니, 삼차 함수 곡선과 그 위의 한 점을 지나는 기울기가 -1일 직선으로 이루어져 있다.
(여기서 중요한 것은 기울기가 -1이면서 점 (t, f(t))를 지나는 직선의 표현을 이해하고 있어야 한다, 참고로 그런 의미를 갖고 있다면 의미에 맞게 표현을 준다. 그리고 잘 이해하고 있다면 생각하지 않아도 그렇게 읽힌다. 직선을 표현 하면서는 절대 f(t)-(x-t)와 같이 주지 않는다는 것이다. 231122의 (가)조건을 직선으로 해석되지 않는 이유도 그렇다...)

231122(가) 조건 - 참고용
3) 이때 t의 위치에 따라 넓이가 달라짐을 이해했을때 기울기가 -1인 접선에서 최댓값을 갖는다는 추측을 할 수 있는데... 확실한가?
그렇지 않다. 이 문제에서 아주 운좋게 됐을 뿐이고, 그런 학생도 맞출 수 있도록 함수를 만들어 준것이다. 출제 의도도 이런 추측을 할 수 있는가에 대해 묻는 것일 것이다. 따라서 문제를 푸는 시험장에서는 이렇게 푸는 것이다.
평가원은 언제나 부모의 마음(제발 맞혀줘...)으로 출제한다. 그런데 서술형이거나 논술 문제로 나왔다면 정당화 과정을 거치지 않을 경우 감점일 것이고, 문제를 해설하는 사람이라면 이런 이야기는 해줘야하는것 아닌가....? 이제 이 문제를 통해 다른 문제를 맞혀야하는데...
사실 수학2의 고려 대상이 아닌 변곡점이 0과 6사이에 있고 이 변곡점에서의 기울기가 -1이면... 그보다 x좌표가 가장 큰 지점에서...최댓값을 갖게 된다. 하지만 이런것을 학생에게 요구하는 것이 아니다.따라서 6을 t범위에서 빼준 것이고, 또한 답이 되는 접선의 방정식이 (9,0)을 지나기도 하기에 정확하게 정당화 과정을 거치지 않고 답을 맞출 수 있긴 할 것이다.
4) 즉, 3탄에서 이야기 했던 맞힌 문제를 소재로 공부한다는 의미로 우리는 '추측을 정당화' 해보려고 한다. (언제나 이 문제를 맞히기 위한 것이 아니라 이 문제를 통해 앞으로 나올 문제를 맞춰야 하기 때문이다) 그렇다면 어떻게 정당화 했는가? 문제에서 f(x)를 인수분해 해서 주었으므로 근을 가지고 그래프를 그리고 기울기가 -1인 직선을 긋는다. 아주 운이 좋다면 그림으로 바로 풀렸을 것이다. (느낌으로 알았겠지만 '유클리드 5번 공리인 부분은 전체보다 항상 작다'로 정당화했다면...) 묻는 것을 이제 식으로 나타내보자.

이것을 미분하여 최댓값을 찾아 정당화 한다.

5) 이후에 연산이다.
1탄 [글의 시작 - 묻는 것에 따라 어떻게 계획하고 행동을 할 것인가 생각하자]
2탄 [해설지가 뭐 이래...? 해설이 아니라 계산지 아닌가....? (feat. 수능 13번)]
3탄 [수능 5번, 맞힌 문제로 공부하기]
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
벡터 하다가 머리 다뽑힐거 같아서 벡터만 버티면 될줄 알았는데 공간도형 오니까...
-
원과목 안했고 나보다 대학 높게 갈 예정인 자만 돌을 던지셈 수시는 나가있어
-
둘레도 같이 써주세요
-
1월 공통 복습하고 2월부터 확통이랑 같이 하려는데 괜찬ㅇㅎ나요?
-
매일 4시간 공부하면서 6시간 자는 게 매일 8시간 공부하면서 4시간 자는 것보다...
-
안그래도 돈도없는데
-
ㅈㄱㄴ
-
내일 전화를.. 아니 근데 학원비 왤케 비쌈요 용돈의 n배나 되네..
-
할코디언 1
ㅇㄴ 그거 뭔데 ㅎㅋㅅ 변형이라고 나무위키에 있는거냐 개끔찍할거같은데 본사람있음??
-
솔직히 241110도 그냥 2분컷냈어서 그냥 이렇게이렇게 풀면 당연한건데 싶지만...
-
여붕이구한다 ㅇㅇ
-
망했다 4
2년 된 버즈 잃어버림
-
원장연 원장연하는거 ㅈㄴ 긁히네
-
내가 쓴 과만 폭인 것 같네....... 다른 데 넣었음 최초합인데 허허 추합이라도...
-
과탐이 재밌음... 표본이 고여도 잘하면 그만
-
집 근처에 (목동,강남권x) 꽤나 지점 많은 브랜드의 관리형 스카 새로운 지점...
-
중시경건 3
마음이 따뜻해지고 경건해지는 참 좋은 말이다
-
근데 점공이 2
한꺼번에 몇명 들어왔다가 또 하루종일 정체네요.. 이제 진짜 쓸 사람들 다 쓴건가
-
재밌군
-
해볼까 Yoon's 가르칠순 있는데 가르쳐도 되나?
-
1과목 실수들(원장연이라는 나쁜말은 ㄴㄴㄴ) 다 투로 가거나 사탐런치는게 지금...
-
1. ∃원인∀결과(원인→결과) : "모든 결과를 일으키는 어떤 원인이 존재한다."...
-
잇올 6시 오픈하자마자 1등으로 입실하던 시기와 무단지각으로 벌점 60점 쌓은...
-
ㅈㄱㄴ
-
나도 과외 구하고 십다 20
시급 만원에 할 수 잇구요 신촌 쪽에서 30분거리에 허수친구면 좋구요 제가 오르비...
-
문명6 0
오랜만에 해볼까
-
23수능 메타로 갈거임 즉 이번엔 작수와 달리 생판 처음보는 단어낚시질 4 5개...
-
"사회복지학과 지망생" 사복과 출신 반수생: STAY...
-
뜌따이 되는거같노 .....
-
네
-
햄버거는 아직 무리인가봐요
-
CC는 뚫으면 되는거잖아?
-
여붕이내놔 7
여붕이내놔 여붕이내놔 여붕이내놔 여붕이내놔 여붕이내놔 여붕이내놔 여붕이내놔...
-
이정도 표본유입으로도 이렇게 정상화시켰는데 분위기,기본인원수보면 유입량 최소n배증간데과연,
-
난 오르비하려고 수면 시간 줄이긴 함
-
수능 컨설팅 받을려면 어디 학원가서 받는게 제일 좋을까? 1
나름 유명한 큰데 기준으로 말하는거 ㅇㅇ 자기 자신의 위치, 앞으로의 전망, 발전...
-
내신영어 의문점 3
내가 내신 버린 이유가 영어 이년때문임 고1때 지문 풀암기로 존나 빡공할때도...
-
세특은 정상임 그래서 bb일 듯 반박시 니말이 틀림 제발
-
과탐2에서 과탐1오는걸 원런이라고 부름? 아니잖아 그냥 사탐이 당연한거고 과거...
-
필수본 교재없이 0
인강만 들으면 안되나? 완자 이미 있는데 사야하나?
-
자유대한~~~ 0
그냥 갑자기 써봄...
-
U치환 0
행복 유치환 사랑하는 것은 사랑을 받느니보다 행복하나니라 오늘도 나는 에메랄드 빛...
-
기하 과외 구합니다 17
각각 22 23 25수능 22번틀 100점 22번틀입니다 시급2 대학 성균관대...
-
여캐일러 투척 18
이거나 올려야지
-
물1 왜 버림? 4
안 씻기만 해도 되는 과목인데
-
커하 4
교육청 76 99 2 99 98ㅠ 역시 오르비라 그런가 다들 너무 고능함...
-
ㅋㅋ 1
ㅋ





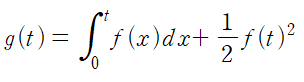
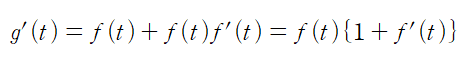






















































수학 100점을 목표로 하고 있는데 수놀음님으로 수학에서 새로운 깨달음을 얻어서 감사합니다.. 제가 기출분석을 하면서 231122는 어떻게 분석해야 할지를 정말 모르겠는데 수놀음님의 관점으로 알고 싶은데 유튜브에 올라갈 예정 있으신가요?
이런 댓글이 있었군요... 수도 없이 수업했던 내용인데 다음 수업 때 한번 찍어서 올려보겠습니다.